算法分享（二）

一个简单的算法题目分享

最近还是在忙百度之星的事，虽然知道进不去决赛，但还是借此练练算法，这次要分享的是百度之星初赛二的签到题。

原题链接

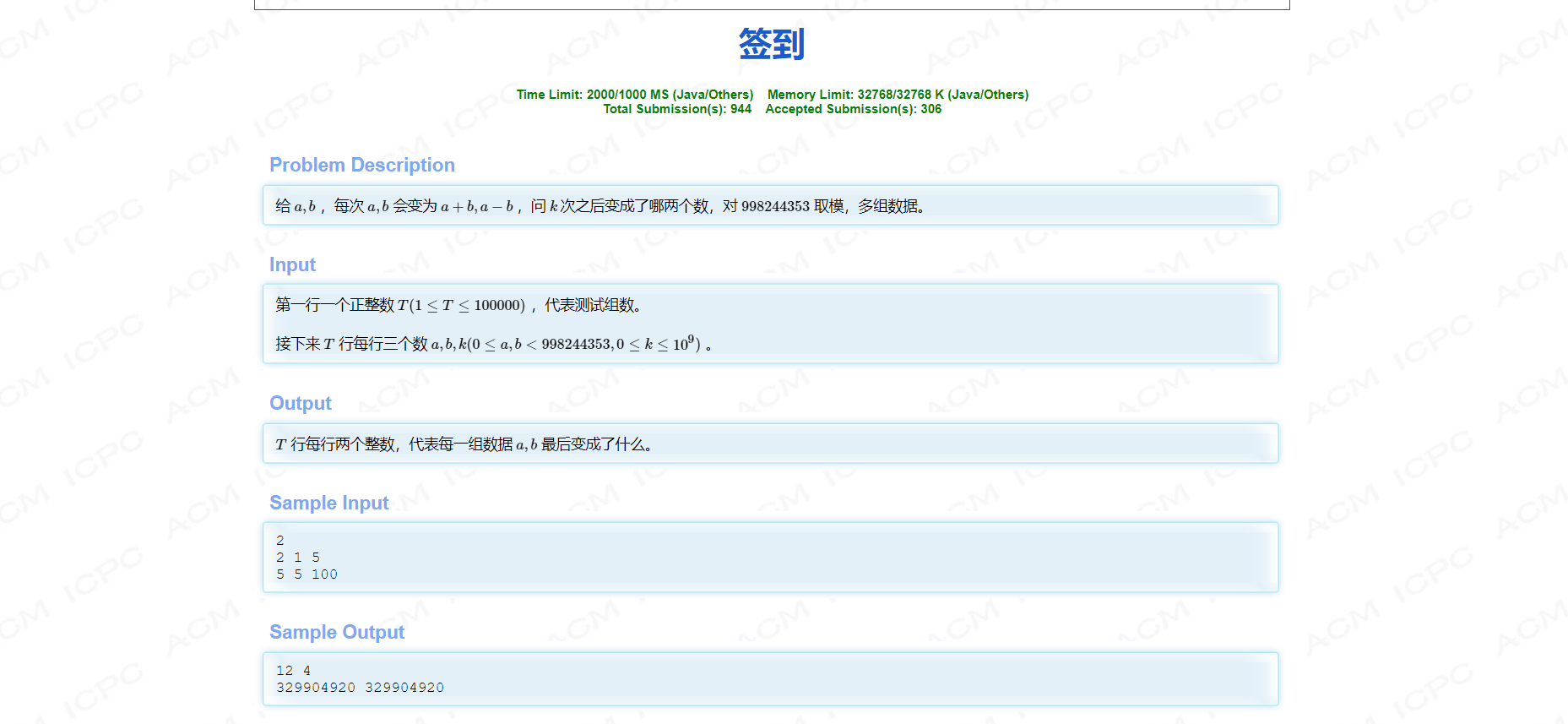
从通过率看并不是一道难题。

其实但从题意上看，本题只要在练习本上多算几个数据，就很容易发现这道题的规律，当k为偶数时，变化后的结果为(2^ k/2)*a，( 2^k/2) *b，当k为奇数时，变化后的结果为（2^ k/2) * （a+b），(2^ k /2)*（a-b)，其实做到这里，我们已经有了解题的思路了，但本题的难点就是数据范围特别大，如果我们不灵活运用取余，那么肯定会超long long，同时我们也必须会使用快速幂，这样的话也不会超时。

#include <stdio.h>
#include <iostream>
#include <algorithm>
#include <math.h>
using namespace std;
int mod = 998244353;
long long quickpow(long long x) //快速幂
{
    long long s = 1,n = 2;
    while(x)
    {
        if(x % 2)
            s = s * n % mod;
        n = n * n % mod;
        x /= 2;
    }
    return s;
}
int main()
{
    int t;
    scanf("%d", &t);
    while(t--)
    {
        long long a, b, k, c;
        scanf("%lld%lld%lld",&a, &b, &k);
        long long s, s1, ans, ans1;
        s = ((quickpow(k / 2) % mod) * a % mod) % mod;
        s1 = ((quickpow(k / 2) % mod) * b % mod) % mod;
        ans = (s % mod + s1 % mod + mod) % mod;
        ans1 = ((s - s1) % mod + mod) % mod;
        if(k % 2)
            printf("%lld %lld\n", ans, ans1);
        else
            printf("%lld %lld\n", s, s1);
    }
    return 0;
}

希望本次分享可以给各位的学习带来帮助。