算法分享

一个简单的算法题目分享

最近参加了百度之星程序设计大赛，周末要去进行复赛（白给），虽然知道进不去决赛，但还是复习了一下，正好看到一道签到题，可以分享一下。

原题链接

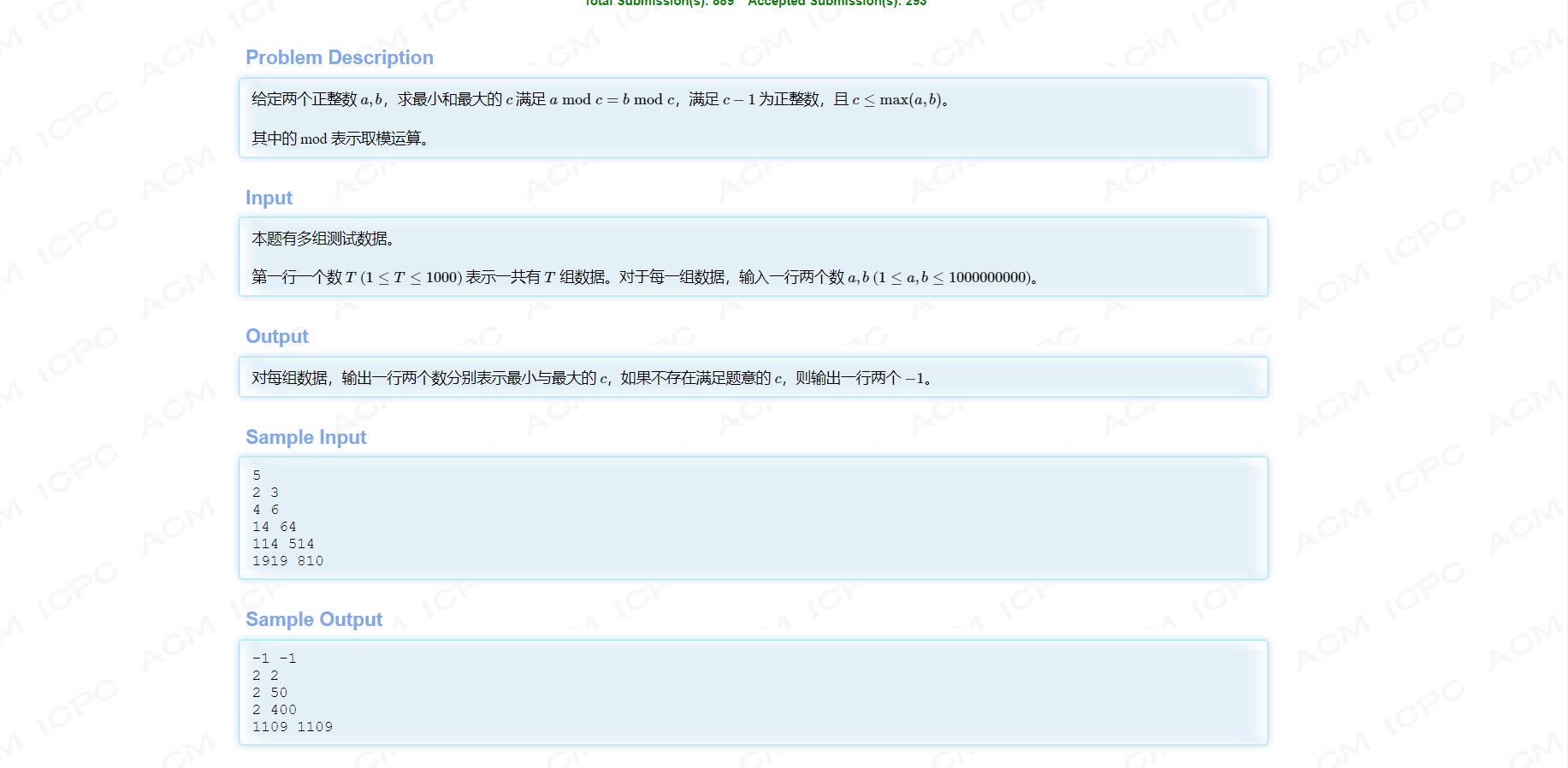
这个题虽然是初赛的签到题，但当时比赛时打出来的并不是很多

其实我相信，很多人如果一拿到手并看懂题意的话，觉得这就是一个找因数的题，只要找到a，b中的公因数就好，直接暴力做法，其实如果本题的数据范围不大，暴力做法就完全可行，那么本题的难度就算是放在ACM新生赛上也只是一道略难于签到题的题，但是这道题的数据范围很大，时间复杂度是O(n)，同时我们提交一下发现也会提示超时，这时候我们就要重新阅读一遍题，看是否可以以快速的方法解决这道题了。

题目要求a%c = b%c，我们可以化成(a - b)%c = 0，这时候，就可以清楚的知道c最大时为a-b，同时题目要求，c-1>0，所以a-b一定要大于1，接下来我们就要寻找c的最小值了，这时候我们在(a-b)中通过找余数的方法所需时间就会大大降低了。

代码：

#include <stdio.h>
#include <iostream>
#include <algorithm>
#include <math.h>
using namespace std;


int main()
{
    int n;
    scanf("%d", &n);
    while (n--)
    {
        long long int a, b, mina, maxa;
        int flag = 0;	//用于做标记
        scanf("%lld%lld", &a, &b);
        mina = 0;
        maxa = 0;
        maxa = max(a, b) - min(a, b);
        if (a == b)
        {
            if (a == 1)		//特判是否全为1，根据题意知c最小为2，如果全为1，便不和题意
            {
                mina = -1;
                maxa = -1;
                flag = 1;
            }
            else
            {
                mina = 2;
                maxa = a;
                flag = 1;
            }
        }
        else if (maxa == 1)		//判断插值是否大于1
        {
            mina = -1;
            maxa = -1;
            flag = 1;
        }
        else
        {
            int i;

            for (i = 2;i <= sqrt(maxa);i++)		//寻找(a-b)的余数
            {
                if (maxa % i == 0) {
                    mina = i;
                    flag = 1;
                    break;
                }
            }
        }
        if (flag == 1)		//根据是否找到最小余数进行不同的输出
            printf("%lld %lld\n", mina, maxa);
        else
            printf("%lld %lld\n", maxa, maxa);
    }
    return 0;
}

希望本次分享可以给各位的学习带来帮助。