实验室暑期考核

第一题

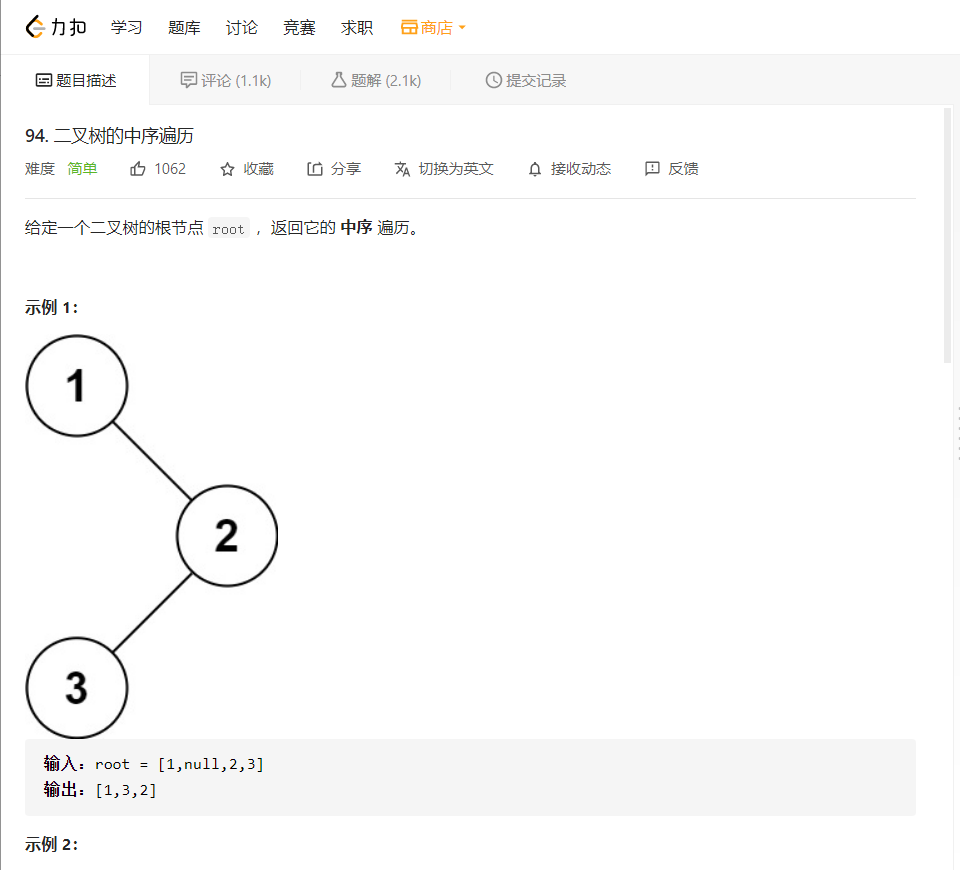
通过分析题意，我们不难看出，这是一个十分经典的算法，经典到上学期的一个重点就是对二叉树进行一个前中后序的遍历。

根据我们的知识，无非就是运用递归算法，一直寻找左子树，直达寻找到叶子节点，将它存放到栈中，再把它的父节点存放到栈中，之后再寻找父节点右子树的左子树。

代码：

class Solution {
public:
  vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ret;
        stack<TreeNode*> toTraversal;
        while(root!=NULL || !toTraversal.empty()){
            while(root != NULL){
               toTraversal.push(root);
               root = root->left;
            }
            root = toTraversal.top();
            toTraversal.pop();
            ret.push_back(root->val);
            root = root->right;
        }
        return ret;
  }
};

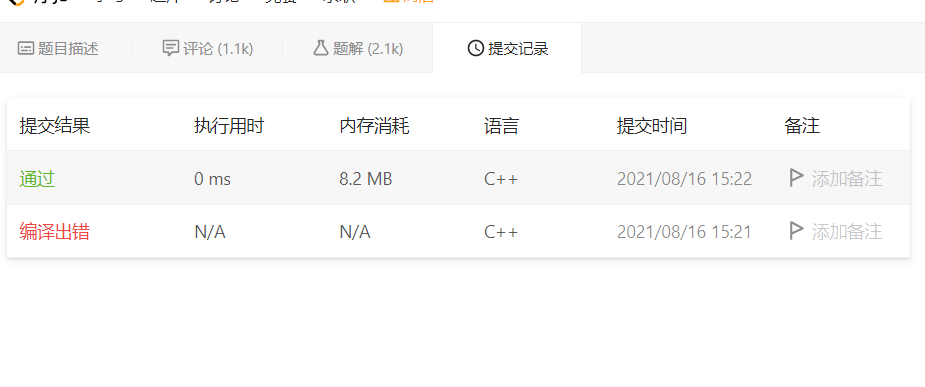
第二题

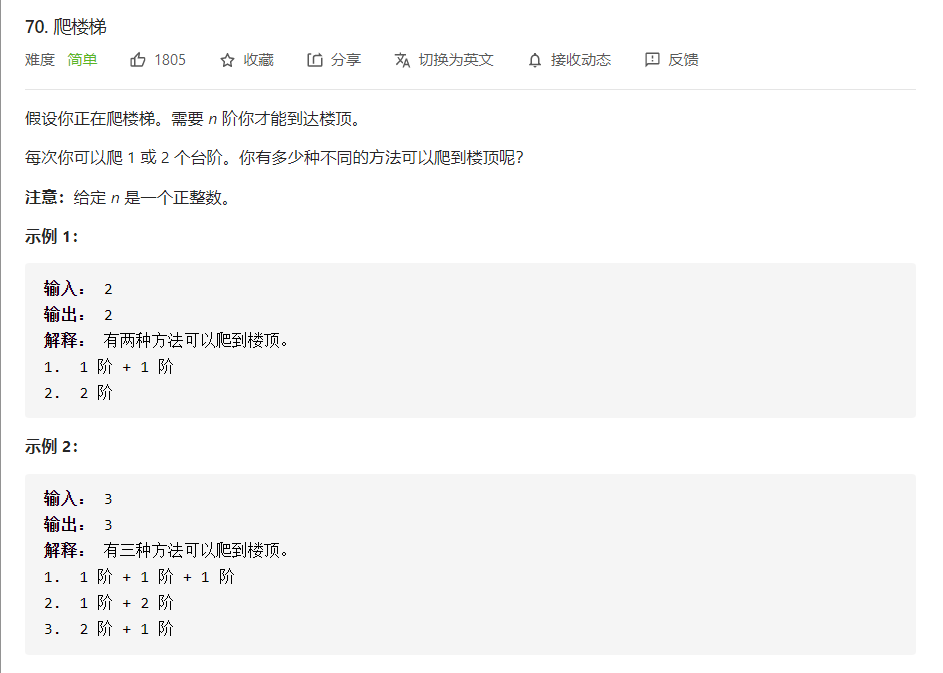
第二题其实本来做过一个类似的，所以我直接用之前的递归思路写：

class Solution {
public:
    int climbStairs(int n) {
        int a;
        if (n == 1)
            return 1;
        else if (n == 2)
            return 2;
        else {
            vector<int> a(n + 5, 0);
            a[1] = 1;
            a[2] = 2;
            int i;
            for (i = 3;i <= n;i++)
            {
                a[i] = a[i - 1] + a[i - 2];
            }
            return a[n];
        }
    }
};

但你会神奇的发现它超时了

所以总结一下，如果直接用递归，时间复杂度回收O(n2)，我们需要换一下，如果你用递归打一下表，会发现它每一阶都是前面两阶的和，这样就可以使用动态规划的方法，使时间复杂度降到O(n)了

class Solution {
public:
    int climbStairs(int n) {
        int a;
        if (n == 1)
            return 1;
        else if (n == 2)
            return 2;
        else {
            vector<int> a(n + 5, 0);
            a[1] = 1;
            a[2] = 2;
            int i;
            for (i = 3;i <= n;i++)
            {
                a[i] = a[i - 1] + a[i - 2];
            }
            return a[n];
        }
    }
};

第三题

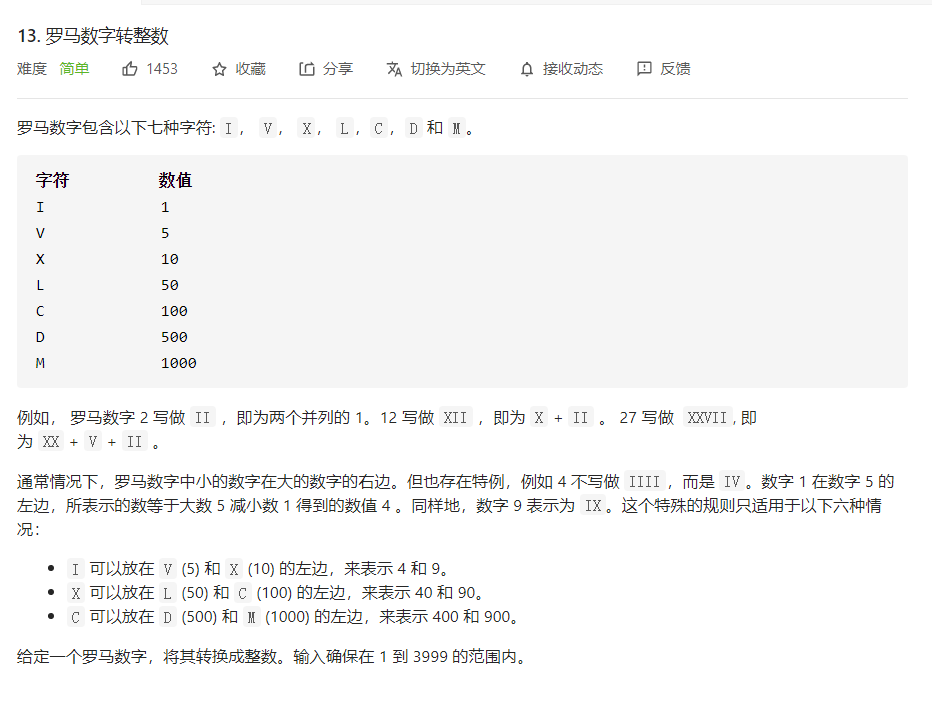
通过本题，不难发现其实是一个字符串识别的问题，并不是特别复杂，只要考虑清楚位置问题用switch就能很好的解决

class Solution {
public:
    int romanToInt(string s) {
       int count = 0, t = 0, flag = 0;	//分别用于计数和标记
       int i;
       for (i = s.length();i >= 0;i--)
       {
        switch(s[i]) {		//获得其中的单个字符
        	case 'I': 
        		t = 1;
        		if(flag == 1) {		//判断是否在V的左面，如果在，则需减去
        			t = -t; 	
        			flag = 0;
        		}
        		break;
        	case 'V': flag = 1; t = 5; break;
        	case 'X': 
        		t = 10;
        		if(flag == 2) {
        			t = -t;
        			flag = 0;
        		}
        		flag = 1; 
        		break;
        	case 'L': flag = 2; t = 50; break;
        	case 'C': 
        		t = 100;
        		if(flag == 3) {
        			t = -t;
        			flag = 0;
        		}
        		flag = 2; 
        		break;
        	case 'D': flag = 3; t = 500; break;
        	case 'M': flag = 3; t = 1000; break;
        	}
        	count += t;
        }
       return count;
    }
};

图片](55566/8.png)